Hệ thống tam giác và tam giác
Câu trả lời và giải pháp Bài 1,2,3,4,5,6,7,8,9 trang 59; Bài 10,11 trang 60 SGK Hình học 10 – Chương 2.
Bài 1. Cho ABC vuông góc với A, góc B = 580 một cạnh = 72 cm. Tính góc C, cạnh b, cạnh c và chiều cao hMỘT
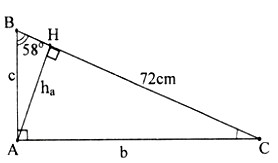
* C = 180° – (∠A + B) = 180° – (90° + 58°)
= 180° – 148° = 32°
* b = AC = BC.sinB = 72.sin58° ≈ 61,06 (cm)
* c = AB = BC.cosB = 72.sin58° ≈ 61,06 (cm)
* c = AB = BC.cosB = 72.cos58° ≈ 38,15 (cm)
* ha =AH = AB.sin58° = 38,15.sin58° ≈ 32,36 (cm)
Bài 2. Cho ∆ABC biết độ dài các cạnh a = 52,1cm; b = 85cm, c = 54cm. Tính các góc A,B,C.
Theo định luật côsin a2 = b2 +c2 – 2 TCN. cosA

=> cosA 0,8089 => góc A = 360

Bài 3.Cho ΔABC ∠A = 1200 Cạnh b = 8 cm, cạnh c = 5 cm. Tính cạnh a và các góc ∠B và ∠C của Δ này.
phần thưởng: MỘT2 = 82 + 52 – 2.8.5 Hệ số 1200 = 64 + 25 + 40 = 129
=> a = 129 ≈ 11, 36cm
Chúng ta có thể tính góc B theo định luật cosin

Chúng ta cũng có thể tính góc B bằng định luật sin:

Bài 4 trang 59. Tìm diện tích S của tam giác có độ dài các cạnh là 7, 9 và 12.
Quảng cáo
Sử dụng công thức của Heron:
Ta có 2p = 7 + 9 + 12 => p = 14
p – a = 14 – 7 = 7
p – b = 14 – 9 = 5
p – c = 14 – 12 = 2
![]()
≈ 31,3 (đơn vị)
Bài 5. Δ ABC , có góc A = 1200. Tính cạnh BC cho cạnh AC = m và AB = n.
Ta có: BC2 = dòng điện xoay chiều2 + AB2 – 2AB.AC. cos1200
=> TCN2 = mét2 + n2 – 2tr.n (-1/2)
=> TCN2 = mét2 + n2 + mangan
![]()
Hình 10 trang 59 Bài 6. Độ dài các cạnh của ΔABC là a = 8cm, b = 10cm, c = 13cm
a) Tam giác có các góc tù không?
b) Tính độ dài trung tuyến MA của ∆ABC.
phần thưởng: a) Xét tổng của a2+ Thứ hai2 -C2 = 82+ mười2 – 132 = -5 < 0
Vậy tam giác này có một góc tù C

b) Áp dụng công thức tính trung tuyến ta tính được AM 10,89cm
Bài 7. Tìm góc lớn nhất đã biết ΔABC:
a) độ dài cạnh a = 3cm, b = 4cm, c = 6cm
b) chiều dài cạnh a = 40 cm, b = 13 cm, c = 37 cm
Ta biết rằng trong một tam giác thì cạnh có cạnh lớn nhất là góc lớn nhất nên ở câu a) góc lớn nhất là góc C và ở câu b) góc lớn nhất là góc A

Bài 8 trang 59. Cho ∠ABC biết cạnh a = 137,5cm;∠B = 830 ;C = 570. Tính góc A, cạnh b, c của tam giác.
phần thưởng: Ta có: A = 1800 – (∠B + C) = 400
Áp dụng định luật sin:

Hình 10 trang 59 Bài 9. Cho hình bình hành ABCD có AB = a, BC = b, BD = m, AC = n. Chứng minh: m2 + n2 = 2(một2 + b2 )

Xét ABC có: BO là trung tuyến

Bài 10 trang 60. Hai tàu P và Q cách nhau 300m, từ P và Q thẳng hàng với chân A của ngọn hải đăng AB trên bờ biển, người ta thấy chiều cao ngọn hải đăng AB góc BPA = 350 Góc BQA = 480
Tính chiều cao của tháp.
trả lời:

Bài 11. Để đo chiều cao chùa Chăm Por Klong Garai ở tỉnh Ninh Thuận, người ta lấy hai điểm A và B trên mặt đất, cách AB = 12 cm, thẳng hàng với chân tháp C, rồi đặt hai thước đa giác. Chiều cao đáy của tam giác là h = 1,3 cm. Gọi D là đỉnh tháp, hai điểm AĐầu tiên, loại bỏngười đầu tiênphù hợp với Cngười đầu tiên chiều cao CD thuộc tháp. Người ta đo góc DA1C1 = 490 Góc DB1C1 = 350.
Tính chiều cao CD của tháp.

trả lời: ![]()

Vậy chiều cao của tháp là 22,77 m.





